二分探索は、ソートされたデータを高速に検索できる非常に便利なアルゴリズムです。特に「境界探索」という考え方をマスターすることで、データの範囲を効率的に取得することが可能になります。
この記事では、二分探索を使った境界探索の基本から応用例までを、Pythonのコードとともにわかりやすく解説します。
二分探索とは?
二分探索は、ソートされた配列から特定の値を効率的に探すためのアルゴリズムです。配列を中央で分割しながら探索するため、計算量は O(logN)O(logN) と非常に高速です。
境界探索は、この二分探索の応用で、「特定の条件を満たす最初の位置」や「条件を満たさなくなる直前の位置」を探すのに使われます。
境界探索の種類
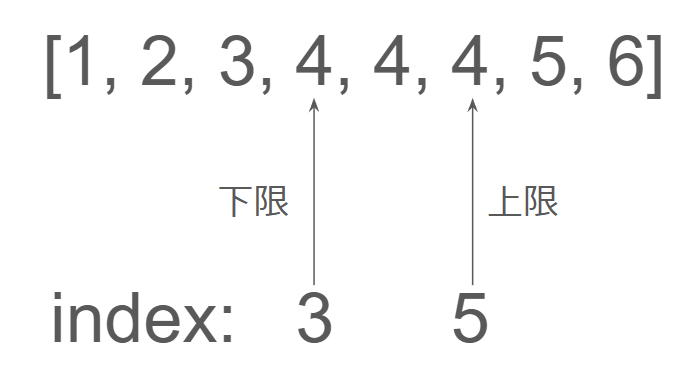
- Lower Bound(下限探索)
特定の値以上になる最初の位置を探します。 - Upper Bound(上限探索)
特定の値を超える最初の位置を探します。
これらを利用することで、例えばソートされたデータから特定の値の範囲を効率的に取得できます。
Pythonによる境界探索の実装
Lower Bound の実装
以下のコードは、配列の中で「特定の値以上になる最初の位置」を探す Lower Bound を実装したものです。
def lower_bound(arr, target):
left, right = 0, len(arr) # [left, right)
while left < right:
mid = (left + right) // 2
if arr[mid] < target:
left = mid + 1
else:
right = mid
return left
Upper Bound の実装
次に、「特定の値を超える最初の位置」を探す Upper Bound のコードを見てみましょう。
def upper_bound(arr, target):
left, right = 0, len(arr) # [left, right)
while left < right:
mid = (left + right) // 2
if arr[mid] <= target:
left = mid + 1
else:
right = mid
return left
境界探索の応用例
特定の値の範囲を探す
たとえば、配列の中で特定の値が出現する範囲(開始位置と終了位置)を求めたい場合、Lower Bound と Upper Bound を組み合わせて以下のように実現できます。
def find_target_range(arr, target):
start = lower_bound(arr, target)
end = upper_bound(arr, target) - 1
if start < len(arr) and arr[start] == target:
return (start, end)
return (-1, -1) # 見つからない場合
使用例:
arr = [1, 2, 3, 3, 3, 4, 5, 6]
target = 3
result = find_target_range(arr, target)
print(f"{target} の範囲: {result}") # 結果: (2, 4)
予算内で購入できる商品の最大数
配列に商品の価格リストが与えられているとします。この中から、予算内で購入できる商品の最大数を求めるには、以下のように二分探索を活用します。
def max_items_with_budget(prices, budget):
prices.sort()
left, right = 0, len(prices)
while left < right:
mid = (left + right) // 2
if sum(prices[:mid]) <= budget: # mid個の商品の合計価格
left = mid + 1
else:
right = mid
return left - 1
max_items_with_budget([1, 2, 3, 4, 5], 10) # 最大4個購入できる
max_items_with_budget([1, 2, 3, 4, 5], 3) # 最大2個購入できる平方根の近似値を求める
二分探索を使えば、平方根の近似値を効率的に求めることも可能です。以下の例は、指定した精度まで計算を行います。
def sqrt_binary_search(x):
if x < 0:
return None # 負の数の平方根は存在しない
left, right = 0, x
epsilon = 1e-6 # 精度
while right - left > epsilon:
mid = (left + right) / 2
if mid * mid < x:
left = mid
else:
right = mid
return left
print(sqrt_binary_search(2)) # 1.4142131805419922Pythonの標準ライブラリを使った簡単な実装
Pythonの標準ライブラリ bisect を使えば、境界探索をさらに簡単に実装できます。
bisect の使用例
from bisect import bisect_left, bisect_right
arr = [1, 3, 3, 3, 5, 7, 9]
target = 3
# Lower Bound: 特定の値以上の最初の位置
start = bisect_left(arr, target)
# Upper Bound: 特定の値を超える最初の位置
end = bisect_right(arr, target)
print(f"{target} の範囲: ({start}, {end-1})") # 結果: (1, 3)
境界探索で注意すべきポイント
よくあるミス
- 事前のソート
二分探索は配列が事前にソートされていることが前提で動作します。 - 初期条件の設定ミス
探索範囲[left, right)の設定が不適切な場合、結果がずれることがあります。 - 探索結果の妥当性
取得したインデックスが配列の範囲内に収まっているか確認する必要があります。 - デバッグの重要性
境界探索の条件は微妙な違いでバグにつながるため、結果をログ出力しながら確認すると良いでしょう。
実践的な練習問題
以下のような課題に挑戦することで、二分探索の理解を深めることができます。
- ソートされた配列で特定の値が現れる範囲を求める。
- 配列から特定の範囲
[low, high]の要素を抽出する。 - 与えられた長さの棒を等分する最小のカット数を求める。
- 数学的な関数 f(x)f(x) の最大値や最小値を境界探索で求める。
結論
二分探索はアルゴリズムの基本でありながら、境界探索のように応用することで、より幅広い問題に対応できる強力なツールです。Pythonではシンプルに実装できるため、ぜひ実践的な問題で試してみてください。
この記事が、あなたのプログラミングスキル向上に役立つことを願っています!

