Pythonの標準ライブラリitertoolsには、便利なツールがたくさん詰まっています。その中でも、データの順列(すべての順序で並び替えた結果)を生成するitertools.permutationsは、多くの場面で役立つ関数です。
今回は、このitertools.permutationsを初心者でもわかりやすく解説し、応用例や便利な使い方までをお届けします!

itertools.permutationsとは?
itertools.permutationsは、与えられた要素のすべての順列を生成する関数です。順列とは、要素の並びをすべての可能な順序で並べたものを指します。
基本構文
itertools.permutations(iterable, r=None)
iterable: 順列を作成する元のデータ(リスト、文字列、タプルなど)。r: 順列の長さ(省略時は全要素を使用)。
簡単な例
import itertools
data = [1, 2, 3]
perms = itertools.permutations(data)
print(list(perms))
出力:
[(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)]
基本的な使い方
全要素の順列を生成
リストや文字列のすべての要素を並び替えます。
import itertools
data = ['a', 'b', 'c']
print(list(itertools.permutations(data)))
出力:
[('a', 'b', 'c'), ('a', 'c', 'b'), ('b', 'a', 'c'), ...]
一部の要素だけを選んだ順列を生成
2つだけの順列を生成したい場合は、引数rを指定します。
import itertools
data = [1, 2, 3]
print(list(itertools.permutations(data, 2)))
出力:
[(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)]
実践的なユースケース
アナグラムの生成
文字列のすべての順列を生成して、アナグラムを探します。
import itertools
word = "cat"
anagrams = set("".join(p) for p in itertools.permutations(word))
print(anagrams)
出力:
{'act', 'tac', 'cat', 'atc', 'cta', 'tca'}
辞書と照らし合わせることで、有効な単語を特定するプログラムを作成することもできます。
スケジュールや座席の組み合わせ
会議のスケジュールや座席の順番を組み合わせる際に便利です。
import itertools
people = ['Alice', 'Bob', 'Charlie']
arrangements = itertools.permutations(people)
for arrangement in arrangements:
print(arrangement)
出力:
('Alice', 'Bob', 'Charlie')
('Alice', 'Charlie', 'Bob')
...
順列数の計算と注意点
順列の数は、次の式で計算されます:
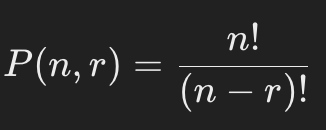
例えば、5つの要素から3つの順列を生成する場合:
from math import factorial
n, r = 5, 3
print(factorial(n) // factorial(n - r)) # 出力: 60
注意点
順列の数は非常に速いペースで増加します。例えば、10個の要素を並び替える場合、その総数は 3,628,800通り です。大規模なデータではメモリ効率を意識しましょう。
関連するitertools関数との比較
以下は、itertools内の主要な関数との比較表です:
| 関数 | 順序の考慮 | 元データの重複維持 | ユースケース |
|---|---|---|---|
| permutations | あり | あり(元データ次第) | 順列、スケジュールの並び替え |
| combinations | なし | なし | チーム編成、宝くじ |
| product | なし | あり | 全組み合わせ、パスワード生成 |
ビジュアルで理解する順列
順列の数がどれだけ速く増えるかを視覚的に示すと、次のようになります。
グラフ生成コード
import matplotlib.pyplot as plt
from math import factorial
n_values = range(1, 11)
perm_counts = [factorial(n) for n in n_values]
plt.plot(n_values, perm_counts, marker="o")
plt.title("Number of Permutations vs Elements")
plt.xlabel("Number of Elements (n)")
plt.ylabel("Number of Permutations (n!)")
plt.show()
このグラフを見れば、要素数が増えると順列の総数が指数関数的に増加することがわかります。
練習問題
学んだことを実践してみましょう!
- 基本問題:
[1, 2, 3, 4, 5]から3つの順列を生成してみましょう。 - 応用問題: 順列の和が10になる組み合わせを列挙してください。
- チャレンジ問題: 辞書と組み合わせて、有効な英単語のアナグラムを探してください。
応用とさらなる学び
順列の考え方は、データ分析、AI、暗号学、ゲーム設計など、さまざまな分野で役立ちます。さらに掘り下げたい場合は、itertoolsの公式ドキュメントや数学的な背景を学ぶことをおすすめします!
Pythonのitertools.permutationsは、シンプルながら非常に強力なツールです。この関数を使いこなせば、データ操作の幅がぐんと広がります。ぜひ試してみてください!

