Pythonでのスライディングウィンドウの効率的な実装方法を解説

スライディングウィンドウ（Sliding Window）アルゴリズムは、データ処理や解析において、ウィンドウサイズを指定しながら効率的に部分データを処理するためのテクニックです。配列や文字列の一部を対象とする計算や検索に特に役立ち、計算量やメモリ使用量を抑えることができます。

この記事では、Pythonでスライディングウィンドウを実装する方法を2つ紹介します：

1. シンプルなリストとmax関数を使った方法（非効率的）
2. collections.dequeを使ったモノトニックデックアルゴリズム（効率的）

両者の違いや計算量についても詳しく解説します。

スライディングウィンドウとは？

スライディングウィンドウは、指定した範囲（ウィンドウ）内のデータを少しずつ移動させながら処理を行う手法です。例えば、次のようなシナリオで活用できます：

• 最大部分配列の和：配列内で、指定したサイズの連続する部分配列の中で最大の和を求めたい場合。
• 文字列のパターン検索：指定サイズの部分文字列が、特定の条件を満たしているかどうかを効率よく調べたい場合。
• 移動平均の計算：時系列データの連続部分を使って平均を求め、データの動向を確認したい場合。

このような問題を効率よく解くため、スライディングウィンドウを用いることで、単純なループを回して部分ごとに全計算し直すよりもはるかに早く処理できることが多いです。

シンプルなリストとmax関数を使った方法

まずは基本的な方法として、リストのスライスとmax関数を使ってウィンドウ内の最大値を求める方法を見てみましょう。

実装例

以下のコードでは、ウィンドウサイズkで順にウィンドウをスライドさせながら、各ウィンドウ内の最大値を取得してリストに追加しています。

def max_sliding_window(nums, k):
    result = []
    for i in range(len(nums) - k + 1):
        window = nums[i:i + k]       # ウィンドウ内の要素を取得
        result.append(max(window))   # 最大値を計算して結果に追加
    return result

# 使用例
nums = [1, 3, -1, -3, 5, 3, 6, 7]
k = 3
print(max_sliding_window(nums, k))  # 出力: [3, 3, 5, 5, 6, 7]

この方法の計算量

ウィンドウを一つ右に移動するたびに、その範囲内の要素に対してmax関数を適用するため、各スライドごとにO(k)の計算が必要です。ウィンドウの移動回数はn - k + 1回（nは配列の要素数）となるため、全体の計算量はO((n - k + 1) * k)となります。

この方法は、ウィンドウサイズkが大きい場合やデータ量が多い場合には、毎回のmax関数の再計算がボトルネックになり、処理が遅くなってしまいます。

dequeを使ったモノトニックデックアルゴリズム

次に、collections.deque（デック）を使った効率の良い方法を紹介します。この方法は、モノトニックデックアルゴリズムと呼ばれ、ウィンドウ内の要素を降順に並べたデックを管理することで、スライドごとに効率よく最大値を取得します。

実装例

from collections import deque

def max_sliding_window_deque(nums, k):
    result = []
    deq = deque()  # インデックスを格納するデック
    
    for i in range(len(nums)):
        # デックの左端にある要素がウィンドウ外に出たら削除
        if deq and deq[0] == i - k:
            deq.popleft()
        
        # デックの右端にある要素が現在の要素より小さければ削除
        while deq and nums[deq[-1]] < nums[i]:
            deq.pop()
        
        # 現在のインデックスをデックに追加
        deq.append(i)
        
        # ウィンドウサイズがk要素以上になったら結果に最大値を追加
        if i >= k - 1:
            result.append(nums[deq[0]])
    
    return result

# 使用例
nums = [1, 3, -1, -3, 5, 3, 6, 7]
k = 3
print(max_sliding_window_deque(nums, k))  # 出力: [3, 3, 5, 5, 6, 7]

図解

ステップ１～２

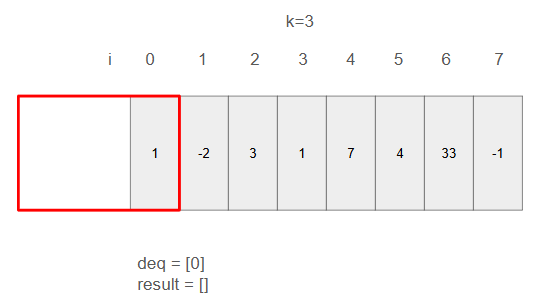
この段階では、deqにインデックスが増えるが、ウィンドウサイズkよりdeqの対象要素数の方が少ない。よってresultは空のまま。

ステップ３

deqの一番右の値が左の２つよりも大きいため、deqの要素は2になる。
deqの対象要素数とkの値が一致したのでresultにはdeqの最大値が入る。

ステップ４

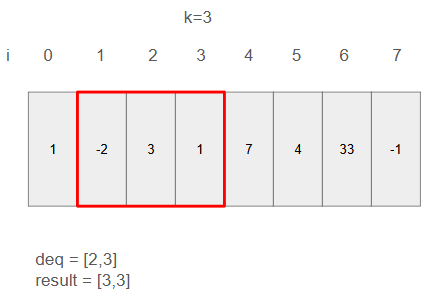
i=3の値（１）がi=2の値（３）よりも小さいため、deqの左に追加される。
resultに入る値は３のまま。

ステップ５

i=4の値（7）がdeqの対象要素の中で最大となるのでdeq=[4]となる。resultには7が入る。

ステップ６

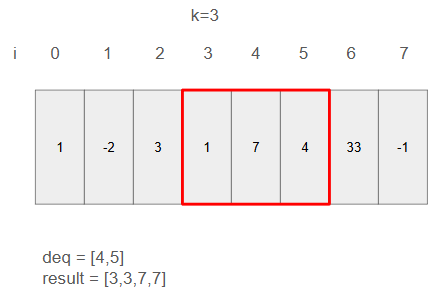
i=5の値は7より小さいためdeqに5を追加、resultには7を追加

ステップ７

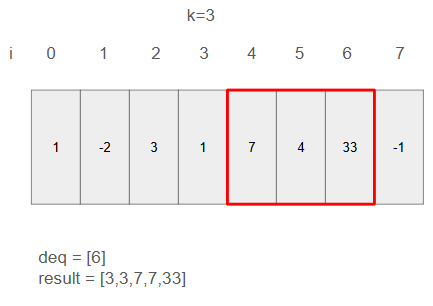
i=6の値（33）が既存deqの値より大きいのでdeq=[6]となる。resultには33が追加される。

ステップ８

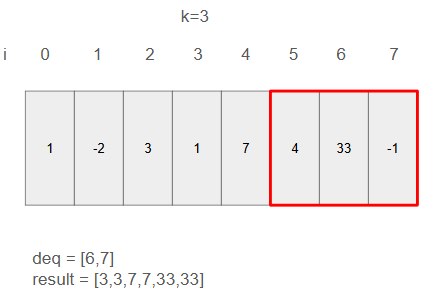
i=7の値は33より小さいためdeqに7を追加、resultには33を追加。

この方法の計算量

このモノトニックデックアルゴリズムでは、各要素はデックに一度だけ追加され、一度だけ削除されるため、計算量はO(n)となります。デックを使うことで、現在の最大値を保持しつつ、ウィンドウの移動ごとに最大値を取得できるため、max関数を毎回使用する必要がなくなります。

両者の比較

まとめ

スライディングウィンドウの実装には、シンプルなmax関数を使った方法と、モノトニックデックアルゴリズムを使った方法があります。前者は実装が簡単ですが、ウィンドウサイズやデータ量が増えると非効率的です。一方、モノトニックデックアルゴリズムを使用すれば、効率的にスライディングウィンドウ内の最大値を管理できるため、大規模データやリアルタイム処理にも適しています。

スライディングウィンドウのようなデータ処理において、効率の良いデータ構造を選択することは重要です。Pythonでスライディングウィンドウを実装する際には、特に処理速度やメモリ使用量が問題になる場合、dequeを活用したモノトニックデックアルゴリズムを検討してみてください。